Alex J. Champandard
The model discussed in the previous tutorial uses the raw input from the distance sensors. That is to say the complete distance to the nearest wall or obstacle is used, no matter how far it is. Admittedly, this value is rescaled for it to be in the neighbourhood of 1, which is convenient for the neural network. This works fine, as the experiments and the demo have already shown!
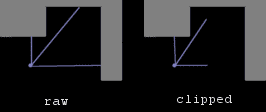
Figure 2: The agent's input based on raw distance measurements (left), and clipped values (right).
However, by observing the best bots avoid walls, it becomes clear that they primarily react to the close proximity of an obstacle. The remaining distances are probably used just to decide the direction to turn into. As an empirical observation, this is not really backed by any scientific evidence, but I'm confident that an analysis of the mapping of input space would also reveal these facts.
Additionally, since our distance sensors are simulated, our solution benefits in efficiency when a maximum distance is set. Specifically, when only say 8 steps need to be taken, the average time taken by the movement simulation will be much more homogenous. Together with this, numerous previous models use clipped distance sensors measurements since they are easier to deal with.
We can take into account another fact to assist the neural network's learning, and that's urgency. This is reminiscent of Craig Reynolds work on steering behaviours and brake forces, but it should be underlined that his approach is explicit. Our approach will be much more implicit, by simply hinting at the neural network that a quick decision should be made.
Basically, we take the clipped distance sensor measurements and scale them so they are always in the range [0..1]. We then simply flip the value (so that 1 indicates a very close obstacle) and square the result:
input = (1 - dist) * (1 - dist)
This doesn't tell the network about urgency, it simply assists its learning of the concept. As we will discuss below in this page, this has nice advantages for our model.
This is a very important concept in optimisation generally, and especially crucial when applied to machine learning in robots. Not only does performance of the learning improve when this scheme is used, but the quality of the results is also better. Indeed, we explicitly block out any possible unbalanced solutions by two small lines of code before and after the neural network. This was the main reason for introducing the scheme, since a bot that can only turn left is pretty useless!
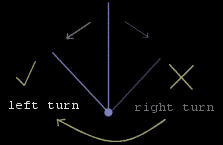
Figure 3: Symmetry removal works by mapping the right portion of the obstacle avoidance search space onto the left side.
I borrowed the idea from a remote field of Artificial Intelligence called constraint satisfaction. The concept is simple: you need to find a combination of variables that solves a problem, and the search tree is very big. To prevent wasted computation, extra constraints are set-up so that the search does not return symmetric solutions. This trims the search space size by at least two, and sometimes even by an order of magnitude.
This also has a great impact on the obstacle avoidance quality: not only can we discard right corners by flipping the neural network's input, but we can also reduce the size of the network thereby! This implies a simpler optimisation problem, and less search time.
In the previous model, only the last output of the neural network was feed back into it. This provided a very small sense of state for the neural network, which allowed it to learn not to change its mind too often (punishing oscillations). This is a good start, but yet more feedback -- or better still, plasticity -- would be welcome.
Initial attempts involved three outputs, two of which were not used except for feedback. Their use was left to the evolution to determine. This was moderately successful, producing bots with passable obstacle avoidance. The most important limitation of this definition was the inability to use symmetry removal.
The next attempt tried to combine three outputs with symmetry removal. One of the feedback output was called the left-state, and the other the right-state. They were swapped when the symmetry conditions were met. This failed with few attempts, but I'm also confident this should work with an appropriate network structure.
Since the neural networks seemed to have very little trouble coping with low speed obstacle avoidance, you can simply artificially boost up the speed of the movement. As a consequence, this provides much more context variety. Not only this, when the solution needs to be applied to a normal speed, the sampling frequency can be halfed, so the movement simulations are not done as often. This is a great economy of processing power.
Speedups of factor 2 were tested, where the bots litterrally sprinted around the level. This worked great, and demonstrated the power of the solution.
Combining all these improvements together drastically improved the overall quality of the model. This could not be judged visibly by checking the behaviour, since the best instances from before and after were very similar. However, big differences were noted in the network sizes. Indeed, the improved models required much smaller neural networks, and generally evolved much quicker. In general, as much as one neural network out of eight (1/8) randomly generated solutions were able to provide above average obstacle avoidance. This was extremely rewarding as a fair amount of time was put into this process.
Many great lessons about neural networks in practice can be learnt from such practical problems, with experimentation and patience being the only required skills
Remember you can visit the Message Store to discuss this tutorial. Comments are always welcome!. There are already replies in the thread, why not join in?