Alex J. Champandard
So how do neural networks fit into the grand scheme of things? What's to stop us from thinking that we're using NN for the sake of it?
First and foremost, if the learning procedure is done correctly the neural network will be able to generalise. This means it will be able to handle scenarios that it did not encounter during training. This is due to the way the knowledge is internalised by the neural network. Also, since the internal representation is neuro-fuzzy, practically no cases will be handled perfectly: there will usually be some small errors in the output values. However, if the learning is successful, the NN will be able to abstract what it has learnt and apply it to other situations. There is no guarantee that this process will estimate the output correctly in all situations, but training the network extensively over a consequent set of varied scenarios can help a great deal.
Secondly, the neural networks can intrinsically handle the types of obstacles and gaps that are presented in front of it, without the need for classifying them. Unlike for other symbolic approaches, the neural network can be given continuous floating point values, without the need for discretisation. As mentioned, this will allow the learning to automatically deal with various kinds of obstacles and gaps.
Thirdly, neural networks are ideally suited to handle random noise. We must admit that our distance sensors will not be perfect - thereby also favouring speed. The neural networks will be able to deal with this noise. Additionally, the training process may voluntarily insert jitter into the sensor data to increase the chances of generalisation. Once again, this is no problem as NN are very fond of this approach.
The fourth point includes that ability to learn unsupervised. This provides us with an undeniable flexibility of the obstacle avoidance module, which can be tuned by setting high-level parameters in the optimisation process (such as clumsiness, laziness, efficiency or appearance of confidence). Not only can these personality parameters be tuned, but we can also use the optimisation algorithm to find the optimal neural network to solve our problem. This implies that we do not need to specify explicitly the behaviour required.
Our fifth and final motivation is efficiency. Simulating a feed-forward network is an extremely fast process, since it involves mainly multiplications. Due to the parallel nature of the neural networks, this can be very easily implemented in parallel, using SIMD or other processor specific instructions. Additionally, we can also manually select the size of the network, and the properties of the layers, so that it is the most efficient.
It now seems beyond doubt that neural networks are an ideal approach to this problem. We still, however, have to determine which specific type of NN is best suited to our obstacle avoidance module.
There are many types of neural network topologies, which specify how the neurons are laid out in the system. Most of these are ill-suited to regression problems, where inputs are combined into one continuous output. One type of network that is suited to this task is called a multi-layer perceptron. It consists of layers of neurons connected to each other in an orderly fashion. The information flows straight from the inputs to the output, with no feedback allowed as in recurrent neural networks. This permits an efficient simulation. It is also capable of handling non-linear problems when the network has two layers and sigmoid activation functions for each neuron.
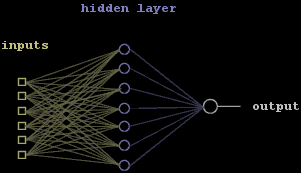
Figure 7: A fully connected multi-layer perceptron. The circles represent individual neurons, and the lines represent weighted connection between those neurons.
More specifically, a fully connected version of this type of feed-forward network will be preferred. Indeed, this will allow heavy parallelisation and minimise the memory overhead. For implementation reasons, we will also prefer layers with a number of neurons multiple of four. This is due to the ability to process four floating-point operations simultaneously with SIMD.
As mentioned, we can also decide the size of the network manually. It could also be optimised with the other parameters of the network, but this is crucial control. We will therefore select a minimal size network, while still allowing good generalisation. Two layers will also be the preferred, but this will not be a hard requirement
Remember you can visit the Message Store to discuss this tutorial. Comments are always welcome!. There are already replies in the thread, why not join in?