Beginners Guide to Pathfinding Algorithms
By ai-depot | December 19, 2002
Heuristically Informed Methods
DFS, BFS and nondeterministic random searches are all fine and good if you dont know anything about the tree you’re searching. If you know even a little bit, though, that knowledge can help you immensely. For one thing, if you know the branching factor and average distance of the paths, you can decide if you should use BFS or DFS.
If you know more than that, for example, distance to goal, you can use that to greatly improve the efficiency of your algorithm.
Given our previous graph,

lets assume each node has the following distances from the goal:

Note, though, that the gray lines represent distance, not actual paths. Using these distance measurements and DFS, we produce a method called Hill Climbing. The psuedocode for Hill Climbing follows:
create a stack P
add the start node S, to P giving it one element
Until first path of P ends with G, or P is empty
extract the first path from P
extend the path one step to all neighbors creating X new paths
If any new paths exist
sort them by their distances from the last node to the goal
reject all paths with loops
push each remaining new path to the FRONT of P
If G found -> success. Else -> failure.
Note the italicized addition. This determines the order they are added to the stack as in DFS (remember before when I said it was a matter of preference? It was then, but now things have changed).
Now we look at the previous example again, with the distances added:
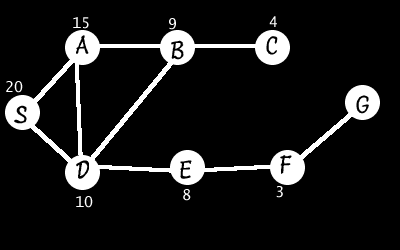
We add S (distance of 20) to the stack and enter the main loop.
Remove S(20), expand it to S->A(15) and S->D(10). We sort these so the shortest remaining path goes first and add them to the stack. So, our stack is now S->D(10) and S->A(15).
Remove the first one, S->D(10), and expand it to S->D->A(15), S->D->B(9) and S->D->E(8) and add them (sorted) to the stack which now has the following: S->D->E(8), S->D->B(9), S->D->A(15) and S->A(15)
Expand S->D->E(8) to S->D->E->F(3) which is still the shortest path so it then gets expanded to S->D->E->F->G and we’ve reached our goal. Note that this takes care of the problem brought up in the DFS discussion. This does not mean that Hill Climbing solves all the problems of DFS, it just happened to find a more efficient path in this one example. In its worst-case scenario, Hill Climbing behaves as DFS.
While the Hill Climbing Method improves the efficiency of DFS, BFS has a potential improvement as well - Beam Search. Beam Search artificially limits the branching factor of the tree to some arbitrary value (for example, 2). This value is denoted W for width of the beam.
The psuedocode for beam search is as follows:
create a queue P
add the start node S, to P giving it one element
Until first path of P ends with G, or P is empty
extract the first path from P
extend ALL PATHS one step to all neighbors creating X new paths
reject all paths with loops
Sort all paths by estimated distance to goal
discard all but closest W paths
push each remaining new path to the BACK of P
If G found -> success. Else -> failure.
The effect of this is it limits the number of neighbors that must be explored to only those that are closest to the goal. The estimated remaining distance is, in most cases the straight-line distance.
However, because the beam search discards potential paths which it never examines again, it may be possible to discard paths which prove more efficient later on or, in some worse cases, discard the only paths to the goal. A very simple example can demonstrate this:
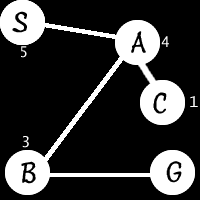
The numbers represent the estimated straight line distance to the goal (these, and most values like this are completely arbitrary numbers I concocted for demonstration purposes) For this example, we’ll assume W is 1, so we only want to explore the shortest estimated distance and ignore everything else.
We start with S which is expanded to S->A. S->A is expanded to S->A->B and S->A->C. We eliminate all but the closest w paths. Since w=1, we keep only the 1 closest path. S->A->B has approximately ‘3′ to go while S->A->C only has one. We put S->A->C into the list and discard S->A->B. Then, on the next loop, we find that S->A->C cant be expanded so we return a failure indicating that no path exists. But, one DOES exist, but our beam search failed to find it. This is where beam search can break down.
Hill Climbing and Beam search both have inherent problems and unless special care is taken (and sometimes its not practicle to monitor the search and make sure its working correctly) they may not find a path, even if one exists. So, there must be a way to use heuristic knowledge in some way to guarantee a path will be found. The solution to this is Best First Search. The psuedocode follows:
create a list P
add the start node S, to P giving it one element
Until first path of P ends with G, or P is empty
extract the first path from P
extend ALL PATHS one step to all neighbors creating X new paths
reject all paths with loops
add each remaining new path to P
Sort entire list P by estimated distance to goal
If G found -> success. Else -> failure.
This is guaranteed to find the path to the goal if any path exists and is likely (though not guaranteed) to do so efficiently. It may follow some unnecessary twists and turns but is still more efficient than BFS or DFS in most cases. In its worst-case scenario, however, it behaves just like BFS.
Tags: none
Category: tutorial |

