Creation of a Simple Sonorant Detector
By ai-depot | November 14, 2002
![]() (goes here)
(goes here)
Written by webmaster.
Creation of a Simple Sonorant Detector
The challenge of automatic speech recognition (ASR) stands at the forefront of computer and cognitive science as one of the more difficult yet promising problems of our time. The problem is based on the observation that speech communication between humans can be described quite accurately using a signal processing model. Speech arrives at a listener�s ears as a pressure wave, borne in some physical medium, usually air. Through a complex and ill-understood series of neural mechanisms, the human listener is able to convert the physical speech signal into a high-level mental object consisting of abstracted linguistic data.
This feat of signal processing is exemplified by a simple experiment: a competent listener presented with a speech signal will be able to write down the words encoded by the signal with almost effortless accuracy. The “words” are a high-level linguistic concept not directly reflected in the speech signal, and yet the human listener can perform the algorithms necessary to convert a pressure wave into a stream of words. This conversion, when performed by a human, satisfactorily solves the speech recognition problem using a biological system.
The goal of ASR is not necessarily to produce a stream of words, given a speech signal. This is a task that would require a much more in-depth examination of the problem and one of which I, unfortunately, lack sufficient knowledge to write an accurate assessment. Instead, I�ll be discussing the problem of broad phoneme identification in a purely academic and fairly simplistic (as far as this problem goes) sense.
Phonemes
Phonemes are atomic linguistic sound units which, when combined in pre-determined high-level ways, formulate words. The knowledg base approach seeks to drive an analysis of the speech signal using linguistic knowledge of the various types of sounds that one expects to surface in a speech signal for a given language. Linguists characterize different phonemes by the features they exhibit. Some of the features which will be discussed, and tested, are obstruance and if the phoneme is �voiced� or not. �Voiced� are sounds that require the vibration of the vocal cords, and obstruance requiring the partial or total blockage of the vocal tract, respectively. All Sonorant sounds are voiced, which provides them with a characteristic which is easily identified. All vowels, nasals (such as /m/, /n/, /ng/), and approximates (such as /l/,/r/,/w/, and /y/) are sonorant. Stops, fricatives and affricates are non-sonorant but some are voiced while others are not.
The hope for ASR is that a system can be built that recognizes the presence or absence of various features, and thereby make positive identifications of various phonemes in a speech stream. This approach is intuitive and reflects the state of the art in linguistic theory.
We simplify our problem somewhat, in the interest of solving a relatively easier problem on the way to achieving a solution for ASR. Linguists group phonemes into larger groups called broad classes:

There are a few more I haven�t included, but this is a fair introduction to them. The only ones I�m concerned with in this article are the mid-row (sonorant, silence and obstruents). Through the rest of this article, I�ll introduce you to a simple sonorant detector.
Test for Sonorance
The test for the presence of sonorance is probably the simplest of the broad phoneme classes to identify and can be characterized simply by +/- sonorance. Sonorance is easily characterized by a periodic sound signal. The presence of a periodic signal is a fairly simple indication of a sonorant sound (including vowels or nasal consonants).
Periodicity can be fairly easily identified based on the autocorrelation function. For our purposes, the autocorrelation function is defined as follows:
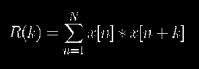
The autocorrelation of a periodic signal will also be periodic, since there will be a point R(k) = R(0) when k=P where P is the period of the periodic signal. The peaks in the autocorrelation will correspond to potentially periodic intervals within the original sound. For a finite but perfectly periodic signal, these peaks will be evenly spaced and will decrease monotonically:

This is due to the fact that as k increases, all the terms from x[n] to x[n + k] will no longer contribute to the sum. This is a rather slow decline in a truly periodic signal and that forms the basis of a simple sonorance detector.
Using this simple function once per every 30ms window is not computationally expensive and, in fact, allows for substantial savings over some of the more complicated alternatives. The simplicity of this method has other advantages as well. First, the signal can be identified as +/- sonorant without the need for training. Second, this has the advantage of being a robust detector despite, or possibly because of, its simplicity. Under noisy conditions, an aperiodic sound becomes even less periodic, making the sonorance identification even easier for the detector, and a periodic signal will still be identified as such by autocorrelation.
In implementing my detector (using matlab and testing off the TIMIT speech database) I used a two-pass procedure. First, a 30ms window (480 samples) moved every 8ms (128 samples) is used to compute the power (Σx[n]2) of each window, which are then normalized by the power of the most powerful window. Any signal windows with a power lower than .001 we can ignore as below the threshold of human hearing.
The second pass, still using a 30ms window moved every 8ms, computes the autocorrelation of that window. Of these, the peaks that fall between 100 and 300 samples form a set P. The human voice has a natural pitch period centered around 115 Hz, so a 30ms window will grab approximately 3 average pitch periods. For all p in P, we compute the ratio:
M(p) = R(p)/R(0)
Followed by:
m = max(M)(0 < m < 1-c)
This m is then becomes the degree of periodicity of a given window which, in our model, is also the probability of this window of the signal being sonorant.
Rather than a probability, we want a labeling of +/- sonorant. Thus, we must define a cutoff to determine how high a probability must be before we label it sonorant or not. After a series of personal tests (by minimizing error over 10 speech files, with varying amounts of noise) I found that .3 was an acceptable threshold. This threshold seems to be independent of voice pitch of speaker. On an average signal, the .3 threshold yields a 6% error rate, which is comparable to more complicated and computationally expensive methods.
This is a very simplistic approach, but it works under simple controlled conditions. To expand this, one could construct two additional detectors: one for nasals and one for stops and thereby classify all major phonetic classes. If the sonorant detector labels a section sonorant, run it through the nasal detector which will declare it to be a nasal or a vowel. If the initial detector labels it as obstruent, the stops detector can label the signal as a stop or a fricative/africative. The first of the following resources is a paper which shows a much more in-depth and thorough method upon which the above discussed simple method is loosely based.
Resources
http://www.dcs.shef.ac.uk/~ljupco/papers/robust.ps.gz
http://www.clsp.jhu.edu/pmla2002/cd/papers/koval.pdf
http://www.elis.rug.ac.be/ELISgroups/speech/cost249/report/references/papers/lin97.pdf
http://www.ee.upenn.edu/~jan/Files/Iscas99Speech.pdf
http://nts.csrf.pd.cnr.it/Papers/PieroCosi/cp-NATO98.pdf
Written by webmaster.
Tags: none
Category: tutorial |

