Decision Trees and Evolutionary Programming
By ai-depot | December 4, 2002
Evolutionary Programming
Evolutionary Programming
In order to address the possibility that a locally sub-optimal partitioning of the data set may lead to an enhancement in the choices for splitting later, I proposed to utilize Evolutionary Programming for tree induction. A complete explanation on the theory of Evolutionary Computation (including Genetic Algorithms, Evolutionary Computation, Evolution Strategies, and Genetic Programming) is beyond the scope of this paper (see Back 1999 and www.ai-junkie.com for excellent reviews), Figure 3 illustrates the general concepts used during this project.
Figure 3: Tree induction via Evolutionary Programming.

Briefly, a population of 100 decision trees is generated randomly. The only criteria used during the generation of this initial population is that the resulting trees be valid in their structure, but no constraints are placed on the choices for splitting rules at any time. Each tree is then assigned a fitness score related to the accuracy of the tree and the complexity or size of the tree. The result of combining accuracy and complexity in the fitness score is that small, highly accurate trees receive higher fitness scores while larger and less accurate trees receive lower scores. This effect will become important in the next sections.
From this initial population of trees, 20 are selected based upon their fitness scores. The method of selection used is known as Roulette Wheel selection which is essentially random selection with some bias based upon the fitness score. The overall result is that while the choices are made at random, those trees with a high fitness score have a higher probability of being selected. Those with lower scores can also be selected for further use, however, they are less probable.
For each of the 20 selected trees, the tree is copied and a random alteration, or mutation, is performed on the copy while the original is placed back into the original population. This mutation may involve changing the feature used for the splitting rule at an arbitrary node, or adjusting the numerical value for an arbitrary node within the tree. As with tree generation, there is no bias for the choice of mutation performed. After the modification has been made, the tree is reevaluated and a given a new fitness score. The 20 mutated trees are then placed back into the population giving us a total of 120 members. Finally, the 20 trees with the lowest scores are destroyed. This represents one generation and the process is continued for 1000 generations.
The underlying assumption in this process is that through random selection of trees and random mutation of the selected trees, it is possible that some change will occur which will improve the performance of that tree. By imposing a fitness score which ultimately determines whether a tree lives or dies in the population, we are imposing an evolutionary selection pressure which is translated into an improving population over time.
Results
In order to assess whether this method could generate a decision tree which performed better than the standard method of recursive partitioning, an empirical study was conducted. In this study, a data set was used consisting of 300 chemical structures, and for those structures, it was known whether the chemical compound would break down naturally in the environment or whether it would persist. The features to describe the chemical structures consisted of 31 values computed based upon the compound�s molecular structure. In order to fully evaluate the performance of Evolutionary Programming for tree induction, the data set was split into multiple groups. The first member of any group served as the Test Set and consisted of 30 chemical compounds selected at random from the original data. The other 270 served as the Training Set for tree induction. Ten individual groups were created such that all of the Test Sets were mutually exclusive. This type of analysis is know as 10-fold cross validation, and is a very useful method to validate classifiers of this type.
For each Test Set � Training Set pair, a tree was developed using the standard method of Recursive Partitioning. Additionally, the Evolutionary Programming method was run 10 times for each pair with the best tree selected for each run at the end of 1000 generations. It should be realized that Recursive Partitioning is a deterministic method, i.e., if it is run multiple times with the same Training Set, you are guaranteed to receive the exact same tree each time. Evolutionary Programming, on the other hand, is stochastic or random in nature. As a result, there is a high probability that you will receive different results between runs. This resulted in 10 Recursive Partitioning trees (one for each Training Set � Test Set pair) and 100 Evolutionary Programming Trees (10 for each Training Set � Test Set pair) for which the performances were averaged. Thus, a comparison of the typical performance of each method can be made.
Table 2 illustrates the results obtained for this data set and is representative of various additional data sets that have been analyzed in this manner. From this table you can easily see that the Evolutionary Programming method results in decision trees that are superior to decision trees generated by Recursive Partitioning. Additionally, the complexity of the trees is equivalent as shown by an equal number of nodes and leaves in the resulting trees.
Table 2: Results of Evolutionary Programming and Recursive Partitioning.
| Minimum Node Size = 30 | Training Set (% Accuracy) |
Test Set (% Accuracy) |
Number of Leaves | Number of Nodes |
| Recursive Partitioning | 77.45 | 73.97 | 6 | 5 |
| Evolutionary Programming | 80.34 | 80.50 | 6 | 5 |
In addition to this test, another data set of unrelated compounds for a different chemical test were predicted with an accuracy of 72% (Training Set) and 68% (Test Set) with Recursive Partitioning induced trees, while Evolutionary Programming induced trees gave results of 72% (Training Set) and 72% (Test Set). These results are not as significant, however, the trend is the same and show that on average, trees produced by this Evolutionary Programming method out perform those produced by the standard method.
Conclusions
While the field of pattern recognition and classification has been an area of research for many years, it is obvious that we are still only beginning to address the potential utility of this field. In this paper I have shown how Evolutionary Programming applied to development of decision trees can produce classifier that are highly accurate and generalizable to data outside the original training set. In comparison to the standard method of decision tree induction, the evolutionary method consistently produces trees that are more accurate and of similar complexity. Further studies involving additional data sets from various problem domains are currently underway and the preliminary results are promising.
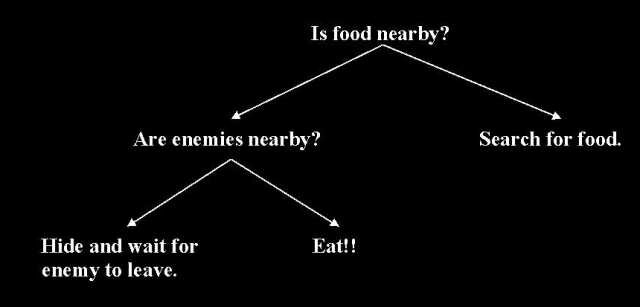
In addition to classifier development, work is underway to develop control systems in a similar fashion. In this case, the decision trees are used to evaluate the current status of the environment and make decision upon what course of action to take. An overly simplistic example is represented in Figure 4. While a preexisting training set does not necessarily exist, the same principles can be used to develop these control systems. It is obvious that establishing the fitness score of any particular tree will require monitoring its performance within an appropriate environment and then determining the outcome. Considering the encouraging results obtained in the classification example, developing valid control system should also be fruitful.
Figure 4: A decision tree used as a control system.
References
Back, Fogel, Machalewicz. Evolutionary Computation I and II. Institute of Physics Publishing, 1999.
Breiman. Classification and Regression Trees. CRC Press, 1984.
Murthy. Automatic Construction of Decision Trees from Data: A Multi-Disciplinary Survey. Data Mining and Knowledge Discovery 2:345-389; 1998.
Quinlan, Rivest. Inferring Decision Trees Using the Minimum Description Length Principle. Information and Computation 80:227-248; 1989.
Written by Kirk Delisle.
Tags: none
Category: tutorial |

