Getting Darwinian Evolution to Work
By ai-depot | February 12, 2003
The Darwinian Evolution Method
The Darwinian Evolution Method
The first requirement is for a viable Darwinian evolution process that can create sophisticated computer software adapted to an environment. This makes use of the concept of architecture machines.
Definition of an Architecture Machine
An architecture machine is a computer that acts on an array of symbols.
The behaviour of an architecture machine is determined by two things:
- Its own internal logic
- The particular array of symbols presented to it.
An architecture machine has a �read/write cursor� that it can move to any position in the array. It can read the symbol at the position of the read/write cursor and it can also write a symbol into the array at the position of the read/write cursor (overwriting any symbol that is already there). (See figure 2)
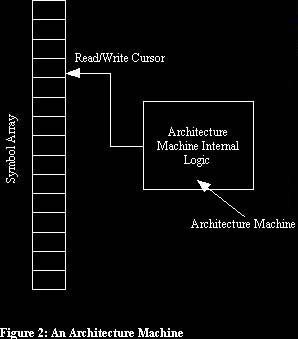
There are similarities with the Turing machine, but a Turing machine is actually a special case of an architecture machine. In particular, the internal logic of a Turing machine works in a very specific way, using an extremely limited number of states, and the read/write cursor of a Turing machine is limited to moving only one element left or right in the array in any one step. Any architecture is valid for an architecture machine and the read/write cursor can be moved from any position in the array to any other position, provided that the architecture machine�s internal logic and inputs/outputs can do this.
Only a limited number of symbols are valid in the array that an architecture machine processes, and I define the number of such symbols as the base of the architecture machine. As an example, an architecture machine which acted on an array of binary digits would have a base of 2. An architecture machine which acted on an array containing the digits 0,1, 2 and 3 would have a base of 4.
Any computer can be used as an architecture machine, provided that it has an adequate number of inputs and outputs that can be interpreted as the required inputs and outputs of an architecture machine (i.e. to move the read/write cursor symbols).
An architecture machine is a computer, but an architecture machine and its symbol array together are also a computer. Particular elements in the symbol array can be interpreted as inputs and outputs. (see figure 3)
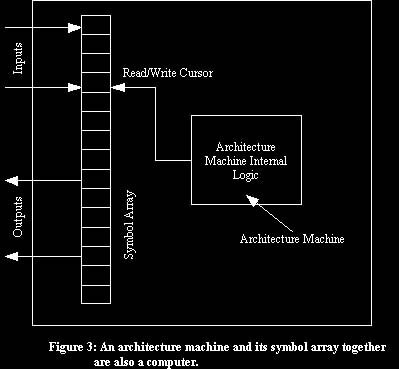
The idea that an architecture machine and the symbol array on which it operates is a computer is really important, regarding what we want to do, because it means that any architecture machine, together with a particular symbol array, can be used together to provide a second architecture machine. This means that if we have an architecture machine and its symbol array then we can interpret specific elements in the symbol array as being the inputs and outputs needed to use it as an architecture machine.
(See figure 4)
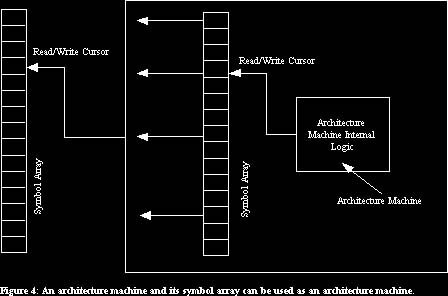
This second architecture machine could act on a second symbol array and the resulting system could be used as a third architecture machine, which acts on a third symbol array, and so on.
A computer can perform a complex task by using such a sequence of architecture machine. The �top level� of the computer would be an array of symbols. This array would be acted upon by an architecture machine, which actually consists of a particular symbol array acted on by an interpretation machine, and so on. (See figure 5)
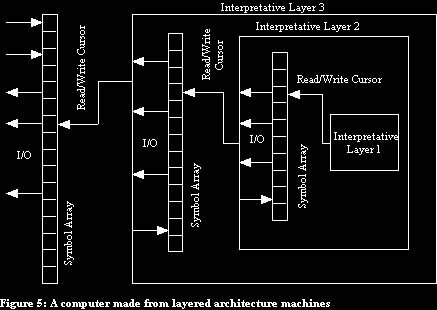
This does not improve the performance of a computer - in fact, use of a large number of interpretative layers is likely to make it run more slowly, so why would we want to do this? The idea is that this can be used a basis for constructing computer software by allowing us to evolve for evolvability and thereby be used to create a sequence of interpretative layers that can ultimately be used to evolve very sophisticated software.
How the Evolution Method will Work
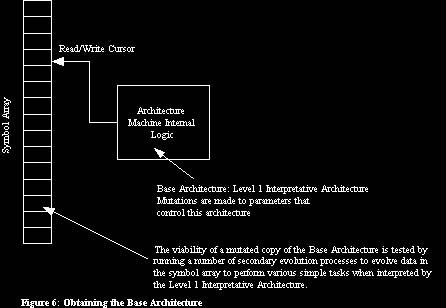
1. Obtaining the Base Architecture
The biological system was based on the laws of physics as its first layer of interpretative architecture. The computer system also needs to have a first layer of interpretative architecture. We will call this the base architecture.
There is no way of generating the entire base architecture by means of any automatic process. This is because any automatic process would need to work by generating a symbolic description of the base architecture. This symbolic description would need to be interpreted by a lower level architecture to have any meaning and this lower level would then actually be the real base architecture. Any automatic method of generating this would in turn have to specify it as a symbolic description and this, in turn, would require a further layer of interpretation. Any attempt to automatically generate the base architecture would therefore involve us in infinite regression.
The base architecture is designed by a human. The base architecture is a set of rules for controlling the read/write cursor as the architecture processes the array of symbols. To keep things simple we will call the array of symbols the �program�.
The base architecture�s rules read the symbol in the program at the cursor position, tell the cursor how to move in the program and control writing of the symbol to the program at the current cursor position.
We cannot generate the base architecture automatically because of the infinite regression problem mentioned earlier, but we can partially automate generation of base architecture. This is done by selecting a particular class of machine for the base architecture and then adjusting parameters that control the behaviour of that machine.
We now need a method of adjusting the parameters of the architecture machine. The method that we will use is Darwinian evolution. We will create a population of architecture machines and make copies with mutations to their parameters. The performance of each architecture machine will be tested and the result of this test will be used to determine whether or not that architecture machine survives in the population to the next generation.
We now need a way of testing an architecture machine to assess its viability. The criteria used is as follows:
The viability of an architecture machine is determined by the rate at which programs (arrays of symbols) can be evolved when that architecture machine�s read/write cursor is used to operate on those programs (i.e. when the architecture machine is used to �run� those programs).
This means that we are running an evolution process in which the test of a successful mutation is to run another evolution process; we are running nested evolution processes. This will make considerable demands on processing time, but I am now convinced that there is no way of avoiding this.
We need to test the evolvability of programs operated on by the architecture machine and, as a matter of fact, we will not do this by attempting just one evolution process, but many evolution processes. Each evolution process attempts to evolve a �program� to complete a different task. This means that we need a large number of tasks, together with methods of assessing success. These tasks should initially be very simple, as a crude architecture is being used to interpret the programs that are being evolved. In fact, to start with, they should preferably be simple enough that some success could be achieved merely by putting symbols together randomly to make the programs.
At the end of the process we will have the parameters needed for the first layer interpretative architecture. In fact, because of the way evolution processes tend to be run, with large population sizes, we may have a number of contenders for the first layer interpretative architecture.
The process for obtaining the first layer is different to the process to be used for subsequent layers, because no lower level architecture is available. When we obtain the second interpretative layer the standard process emerges.
(See figure 6)
2. Obtaining the Second Interpretative Layer
We now have a first layer interpretative architecture. This operates on a �program�, which is simply an array of symbols.
We now regard this first layer interpretative architecture and the �program� on which it operates as together forming a computer and we adapt this computer to allow it to be used as an architecture machine.
Adapting the system to allow its use as an architecture machine simply involves giving it the capability to control an architecture machine�s read/write cursor and to perform read/write operations at the cursor position. This means that certain positions in the symbol array will be selected as inputs and outputs to control the read/write cursor and perform read/write operations.
We have now produced the basis of our second layer interpretative architecture, but we do not have the programming needed to make it actually do the interpreting. This programming is generated by a Darwinian evolution process.
We need to examine what this programming in the second layer will do; it will interpret the programming on the third layer. We therefore use a nested evolution process similar to the one that we used when setting the parameters for the first layer.
We set up a population of machines with various arrays of symbols for the second interpretative layer programming. We produce copies of the machines and, in each of these copies, we make a mutation to the array of symbols in the second interpretative layer. After each mutation we assess the viability of the particular second interpretative layer that is being tested. The viability is assessed according to how well evolution of the symbol array in the third interpretative layer progresses when this particular second interpretative layer is used to interpret it. To assess the mutation, therefore, a number of evolution processes are performed to see how quickly the third interpretative layer can be evolved to solve problems and what level of sophistication can be obtained.
3. Obtaining the Third Interpretative Layer
We now have an array of symbols for the second stage interpretative layer programming. The method for obtaining the third interpretative layer is basically the same.
We make an architecture machine that operates on the array of symbols in the fourth interpretative layer. This architecture machine consists of the third interpretative layer, operated on by the architecture machine formed by the second interpretative layer (which in turn works by being operated on by the first layer interpretative architecture machine).
We make this architecture machine by selecting elements in the third layer array to be used as inputs and outputs to control the cursor that allows it to operate on the fourth layer.
We need to evolve the sequence of symbols for the third interpretative layer. We make mutations to copies of third level arrays and we test the viability of a mutated copy by testing how quickly secondary processes can occur on the fourth level when the architecture machine formed by the third layer (and the layers beneath it) is operating on it and how much sophistication they can produce.
The similarity between this process and the process used to obtain the second interpretative layer should be apparent.
4. Obtaining Subsequent Interpretative Layers
A similar process is used to obtain each successive layer.
To generalise this:
Before we obtain interpretative layer n we first obtain interpretative layers n-1,
n-2,…1.
To obtain interpretative layer n we first set up the system to interpret layer n+1. This means that we make an architecture machine by selecting elements in the layer n symbol array as inputs/outputs, to act as the control interface for the read/write cursor that operates on layer n+1.
The sequence of symbols in layer n is generated by a Darwinian evolution method. A random population of layer n symbol arrays is produced. Populations of mutated copies of the sequence of symbols in layer n are then repeatedly produced from the previous populations. Most of these are discarded, but those considered viable are retained.
The viability of a particular array of layer n symbols is tested by means of a large number of secondary evolution processes. Each secondary evolution process involves attempting to evolve the array of symbols in layer n+1 so that it performs a given task when interpreted by layer n, layer n being interpreted by the layers underneath it. The viability is greatest when the secondary evolution processes proceed quickly and generate substantially sophisticated behaviour.
Tags: none
Category: essay |

